Kerbal Space Programm
schnell genug fallen = endlos kreisen
Es handelt sich um ein Spi... Weltraumsimulator. Ein ganzes Sonnensystem wird abgebildet und simuliert. Da sammeln sich notizen und Berechnungen an, die ich gerne hier teile. Zuerst noch die Review von GameStar. Die YouTube-Kanäle von Matt Lowne (englisch), Scott Manley (englisch) und wintermancer (deutsch) sind sehr zu empfehlen, da ich aus deren Videos viel gelernt habe oder mich inspieren lassen konnte. Rechts in der Sidebar findet ihr direkte Links zu den Inhalten.
deltaV
der Treibstoff, aus dem Träume sind
Budget
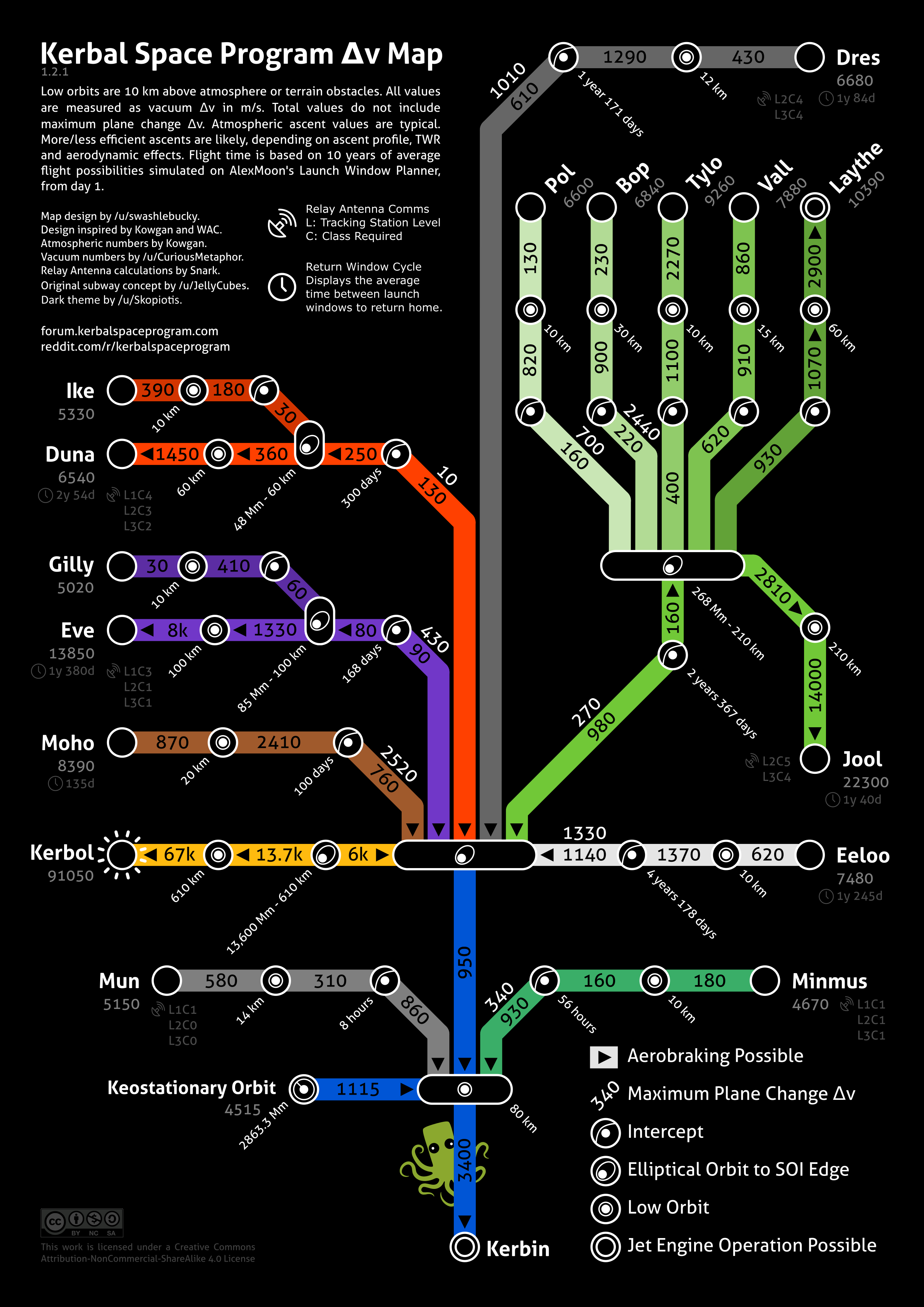
Um sich im All fortzubewegen muss man eine gewisse Masse in eine gewisse Richtung beschleunigen. Dieser Wert wird in deltaV gemessen. Also geht es bei der Planung einer Mission um die Berechnung, wie viel deltaV man benötigt. Und während der Mission ist immer ein Auge auf das deltaV-Budget zu richten. Um deltaV zu erhalten, muss man möglichst viel Treibstoff und möglich wenig Gewicht mit sich schleppen.
Reserven
Ich schlage gerne ein paar Reserven drauf. Denn die Berechnungen gehen natürlich von einem fehlerfreien Burn und einer optimalen Umlaufbahn aus. Das kriegt man in der Regel nie wirklich hin. Nur schon gibt es kleine Abweichungen, weil die Berechnung nicht berücksichtigt, dass das ganze deltaV über einen längeren Zeitraum freigesetzt wird und nicht sofort. Und die Landungen sollen nicht immer mit einem Suicid-Burn enden. Vor allem wenn man ein paar ängstliche Touristen dabei hat.
| Wofür | Wieviel | Beispiel |
|---|---|---|
| Aero-Capture | +10m/s | Eintritt in Kerbins Atmosphäre am Ende |
| Landung | +50% | Landung auf Mun: 870m/s |
| Start | +17% | Start von Kerbin: 3978m/s |
| Interplanetarer Transfer | +100% | Kerbin nach Duna: 260m/s |
Beispiel
Bauen wir also beispielsweise eine Rakete, die auf Minmus landen kann. Wir fangen von hinten an. Am Ende landet nur die Kapsel mit einem Fallschirm. Wir bauen eine Trägerrakete, die uns in den korrekten Orbit um Kerbin bringt. Also brauchen wir auf der Rakete selbst nur das deltaV nach Minmus und zurück.
| Wofür | deltaV | Reserven | Total | verbleibend |
|---|---|---|---|---|
| nach Minmus | 930m/s | - | 930m/s | 2651m/s |
| Minmus-Orbit | 150m/s | - | 150m/s | 1721m/s |
| Minmus-Landung | 180m/s | +50% | 270m/s | 1571m/s |
| Minmus-Start | 180m/s | +17% | 211m/s | 1301m/s |
| Minmus-Flucht | 150m/s | - | 150m/s | 1090m/s |
| nach Kerbin | 930m/s | +10m/s | 940m/s | 940m/s |
Die Trägerrakete bringt uns in den korrekten Orbit und deorbited sich danach selbst wieder. Solltest du sie seperat entwerfen, dann beachte, dass du das Gewicht der Rakete noch berücksichtigen musst.
| Wofür | deltaV | Reserven | Total | verbleibend |
|---|---|---|---|---|
| Kerbin-Start | 3400m/s | +17% | 3978m/s | 4328m/s |
| Plane-Change | 340m/s | - | 340m/s | 350m/s |
| nach Kerbin | 0m/s | +10m/s | 10m/s | 10m/s |
Polarorbit
Einen Orbit vom Äquator um 90° zu auf die Pole zu kippen, benötigt mehr Energie, je näher man sich dem Himmelskörper befindet. Deswegen sollte dies aus einem möglichst hohen Orbit geschehen. Aber diese zu erreichen, benötigt, je nachdem, wo man herkommt, auch viel Energie. Also gibt es noch die Möglichkeit eines exzentrischen Orbits.
| Planet | min. Höhe | deltaV | max. Höhe | deltaV | deltaV (exzentrisch) |
|---|---|---|---|---|---|
| Kerbin | 60km | 3722m/s | 1500km | 1835m/s | 1269m/s |
| Mun | 25km | 761m/s | 1000km | 330m/s | 186m/s |
| Minmus | 25km | 204m/s | 300km | 100m/s | 62m/s |
| Moho | 25km | 1108m/s | 1250km | 475m/s | 264m/s |
| Eve | 70km | 4608m/s | 1500km | 2726m/s | 1963m/s |
| Gilly | 25km | 21m/s | 65km | 15m/s | 12m/s |
| Duna | 32km | 1309m/s | 1500km | 576m/s | 328m/s |
| Ike | 25km | 490m/s | 650km | 219m/s | 126m/s |
| Dres | 25km | 514m/s | 690km | 228m/s | 131m/s |
| Jool | 600km | 9253m/s | 1500km | 8680m/s | 8399m/s |
| Pol | 25km | 145m/s | 220km | 74m/s | 48m/s |
| Bop | 25km | 236m/s | 325km | 113m/s | 70m/s |
| Tylo | 60km | 2926m/s | 1500km | 1641m/s | 1135m/s |
| Vall | 30km | 1122m/s | 1500km | 481m/s | 268m/s |
| Laythe | 50km | 2672m/s | 1500km | 1401m/s | 920m/s |
| Eeloo | 25km | 796m/s | 1050km | 344m/s | 193m/s |
Orbits um Kerbin
Um mein Budget für Satelitten-Missionen besser berechnen zu können, habe ich eine Mission durchgeführt, die folgende Tabelle mir zu erarbeiten. Gemessen wurde immer von einem Orbit auf 80km Höhe von Kerbin aus. Zuerst, wie viel deltaV wird benötigt um die AP zu erreichen. Dies resultiert in einem Orbit mit einer PE von 80km und der AP auf der entsprechenden Höhe. Um auf der AP die PE auf dieselbe Höhe zu heben, wird zusätzlich deltaV benötigt.
| Zielhöhe | AP | Orbit | Gesamt |
|---|---|---|---|
| 200'000m | 90m/s | 90m/s | 180m/s |
| 400'000m | 210m/s | 190m/s | 400m/s |
| 600'000m | 300m/s | 260m/s | 560m/s |
| 900'000m | 400m/s | 330m/s | 730m/s |
| 1'400'000m | 505m/s | 385m/s | 890m/s |
| 2'000'000m | 590m/s | 415m/s | 1'005m/s |
| 3'500'000m | 705m/s | 435m/s | 1'140m/s |
| 6'500'000m | 800m/s | 415m/s | 1'215m/s |
| 25'000'000m | 905m/s | 290m/s | 1'195m/s |
Satelliten
Abtaster
Der Abtaster muss in einen Polarorbit (80°-100°) platziert werden. Er darf nicht näher am Himmelskörper sein als 25km oder 10% seines Radius. Und weiter weg als 1500km oder 500% des Radius ebenfalls nicht. Er überträgt 0.205 Mbits Daten pro km Radius.
| Radius (km) | |
| Minimale Höhe (km) | |
| Maximale Höhe (km) | |
| Daten |
Funk
Relais-Satelitten sind nötig, um auch Regionen mit Funk zu versorgen, die nicht direkt eine Sichtverbindung zur nächsten Station haben. Es schadet sicherlich nicht, solche Satelitten in Orbits von Planeten und Monden zu platzieren. Die folgenden Rechner sollen helfen, die ganzen Berechnungen zu vollziehen. Zuerst aber eine Übersicht der Antennen und deren Leistungen.
| Antenne | Leistung | in m | Kombinierbar? | Typ |
|---|---|---|---|---|
| Pods | 5km | 5'000 | nein | Direkt |
| Experimentüberwachung | 500km | 500'000 | nein | Direkt |
| TRN | 50Gm | 50'000'000'000 | nein | Quelle |
| Communotron 16 | 500km | 500'000 | ja * | Direkt |
| Communotron 16-S | 500km | 500'000 | nein | Direkt |
| Hochleistungsantenne HG-5 | 5Mm | 5'000'000 | ja | Relais |
| Communotron DTS-M1 | 2Gm | 2'000'000'000 | ja | Direkt |
| Relaisantenne RA-2 | 2Gm | 2'000'000'000 | ja | Relais |
| Communotron HG-55 | 15Gm | 15'000'000'000 | ja | Direkt |
| Relaisantenne RA-15 | 15Gm | 15'000'000'000 | ja | Relais |
| Communotron 88-88 | 100Gm | 100'000'000'000 | ja | Direkt |
| Relaisantenne RA-100 | 100Gm | 100'000'000'000 | ja | Relais |
| Sender (Station, Relais) | Empfänger (Raumschiff, Sonde) | |
|---|---|---|
| Stärkste Leistung | ||
| Summe der Leistung | ||
| Effektive Leistung * | ||
| Gewünschte Signalstärke | >0% | 80% |
| Reichweite ** | ||
| Anzahl Satelliten | ||
| Radius des Himmelskörpers | ||
| Gewählte Höhe (m) | ||
| Distanz zwischen Satelliten *** |
Um die Satelliten gleichmässig zu verteilen, empfehle ich alles mit einer Rakete zu starten. Diese muss dann in einen Orbit gebracht werden, wo pro Orbit ein Satellit abgesetzt werden kann. Der Satellit muss dann genug deltaV im Tank haben, dass er vom Absetzorbit seinen Zielorbit erreichen kann. Für die folgende Berechnung wird die Anzahl Satelliten aus der rechten Spalte des obigen Rechners genommen.
| Umlaufzeit | Tage | Stunden | Minuten | Sekunden |
|---|---|---|---|---|
| Satellit | ||||
| Innen | ||||
| Aussen |
| Strombedarf für Antennen | |
|---|---|
| Daten | |
| Paketgrösse (Mit) | |
| Bandbreite (Mit/s) | |
| Strombedarf (pro s) | |
| Datenpakete | |
| Dauer (s) | |
| Batterien | |
Triebwerke
Boosterstufe
Die effizientesten Booster-Triebwerke für die unterste Stufe der Rakete. Diese Stufe sollte die Rakete aus den tieferen Luftschichten herausbeschleunigen. Eine Schub-Gewicht-Verhältnis (SGV) von 1.2-1.5 ist dafür erforderlich. Bis ca. 100m/s sollte die Rakete gerade hoch fliegen. Dann beginnen wir sachte mit einem Schwenk auf der 90° Achse auf ca. 45° Neigung. Unter 7km bleiben wir zwischen 250-300m/s. Danach können wir bis 18km auf 500-600m/s beschleunigen. Dafür verwenden wir Triebwerke mit einer möglichst Hohen Isp in der Atmosphäre.
| Name | Typ | NN Schub | NN Isp | Kosten |
|---|---|---|---|---|
| Mammut | LFE | 3'746.03 | 295 | 39'000 |
| Vektor | LFE | 936.51 | 295 | 18'000 |
| Mastodon | LFE | 1'283.61 | 290 | 8'000 |
| Pf… | LFE | 153.53 | 290 | 3'850 |
| Rotluchs | LFE | 374.19 | 290 | 2'000 |
| Hauptsegel | LFE | 1'379.03 | 285 | 13'000 |
| Kodiak | LFE | 247.00 | 285 | 1'100 |
| Zwillingssau | LFE | 1'866.67 | 280 | 17'000 |
| Skipper | LFE | 568.75 | 280 | 5'300 |
| Welpe | LFE | 28.90 | 280 | 800 |
| Bumms | LFE | 108.20 | 275 | 820 |
| Schraube | LFE | 15.17 | 275 | 230 |
| Nussschale | LFE | 240.91 | 265 | 2'300 |
| Autark | LFE | 205.16 | 265 | 1'100 |
| Funke | LFE | 16.56 | 265 | 240 |
| Spinne | LFE | 1.79 | 260 | 120 |
| Schwenker | LFE | 167.97 | 250 | 1'200 |
| Clydesdale | SRB | 2'948.94 | 210 | 18'500 |
| Rhino | LFE | 1'205.88 | 205 | 25'000 |
| Vollblut | SRB | 1'515.22 | 205 | 9'000 |
| Pollux | SRB | 1'155.56 | 200 | 6'000 |
| Rückstoss | SRB | 593.86 | 195 | 2'700 |
| Garnele | SRB | 26.51 | 190 | 150 |
| Milbe | SRB | 11.01 | 185 | 75 |
| Klopfer | SRB | 250.00 | 175 | 850 |
| Hammer | SRB | 197.90 | 170 | 400 |
| Gepard | LFE | 52.82 | 150 | 850 |
| Floh | SRB | 162.91 | 140 | 200 |
Oberstufe
Nachdem die dichten unteren Luftmassen unter uns liegen, liegt der Orbit vor uns. Dafür müssen wir nicht mehr primär Höhe gewinnen, sondern vor allem an Geschwindigkeit. Diese Stufe sollte die restlichen deltaV für das Erreichen des Orbits enthalten und ein SGV von ca. 1 aufweisen. Ab 18km kann man aggresiver in Richtung 45° Neigung steuern. Zudem halten wir nun die berechnete Apoapsis (AP) im Blick. Für mich hat folgende Faustregel immer sehr gut funktioniert. Ich beschleunige in eine Neigung von soviel Grad, wie die Differenz von 70km zu der aktuellen AP (in 10km-Schritten) ist. Habe ich 18km erreicht und eine Neigung von 45°, warte ich, bis die AP 30km anzeigt und neige auf 40°. Bei einer AP von 40km neige ich mich auf 30°, bei 50km auf 20° und bei 60km auf 10°. Zeigt die AP 70km neige ich mich auf 0°. Der Vektor hinkt meistens immer hinterher und so sollte ich weiterhin an Höhe gewinnen. Wenn nicht, dann kann die Neigung auch auf 5° erhöht werden. Sobald die 80km AP erreicht sind, schalte ich die Triebwerke aus und plane ein Manöver für den Orbit auf der AP und führe diesen wie gewohnt aus. Wir nutzen dafür die Triebwerke, mit einer guten Isp in der Atmosphäre, wie auch im Vakuum.
| Name | Typ | NN Schub | NN Isp | Vak. Schub | Vak. Isp | Kosten |
|---|---|---|---|---|---|---|
| Pf… | LFE | 153.53 | 290 | 180.00 | 340 | 3'850 |
| Mammut | LFE | 3'746.03 | 295 | 4'000.00 | 315 | 39'000 |
| Vektor | LFE | 936.51 | 295 | 1'000.00 | 315 | 18'000 |
| Skipper | LFE | 568.75 | 280 | 650.00 | 320 | 5'300 |
| Rotluchs | LFE | 374.19 | 290 | 400.00 | 310 | 2'000 |
| Hauptsegel | LFE | 1'379.03 | 285 | 1'500.00 | 310 | 13'000 |
| Mastodon | LFE | 1'283.61 | 290 | 1'350.00 | 305 | 8'000 |
| Nussschale | LFE | 240.91 | 265 | 300.00 | 330 | 2'300 |
| Welpe | LFE | 28.90 | 280 | 32.00 | 310 | 800 |
| Kodiak | LFE | 247.00 | 285 | 260.00 | 300 | 1'100 |
| Funke | LFE | 16.56 | 265 | 20.00 | 320 | 240 |
| Zwillingssau | LFE | 1'866.67 | 280 | 2'000.00 | 300 | 17'000 |
| Bumms | LFE | 108.20 | 275 | 120.00 | 305 | 820 |
| Autark | LFE | 205.16 | 265 | 240.00 | 310 | 1'100 |
| Schwenker | LFE | 167.97 | 250 | 215.00 | 320 | 1'200 |
| Schraube | LFE | 15.17 | 275 | 16.00 | 290 | 230 |
| Spinne | LFE | 1.79 | 260 | 2.00 | 290 | 120 |
| Rhino | LFE | 1'205.88 | 205 | 2'000.00 | 340 | 25'000 |
Raumschiff
Für das Raumschiff selbst (oder Sonde, Satellit, ...) welches sich nur im Vakuum bewegt, ist es ziemlich einfach. Das SGV ist nur für eine Landekapsel relevant, ansonsten gilt nur eines: Effizienz. Wenn die SGV extrem niedrig ist, kann aber ein Fluchtmanöver sehr lange dauern. Dauert das Manöver 20min kann man dies auf maximal 5min verkürzen (4facher Physik-Warp). Diese 5min muss man aber dann in Echtzeit verstreichen lassen und darf das Ende nicht verpassen.
| Name | Typ | Vak. Schub | Vak. Isp | Kosten |
|---|---|---|---|---|
| Morgenröte | XE | 2.00 | 4'200 | 8'000 |
| Nerv | NE | 60.00 | 800 | 10'000 |
| Wolfshund | LFE | 375.00 | 380 | 3'000 |
| Gepard | LFE | 125.00 | 355 | 850 |
| Pudel | LFE | 250.00 | 350 | 1'300 |
| Terrier | LFE | 60.00 | 345 | 390 |
| Rhino | LFE | 2'000.00 | 340 | 25'000 |
| Pf… | LFE | 180.00 | 340 | 3'850 |
| Nussschale | LFE | 300.00 | 330 | 2'300 |
| Skipper | LFE | 650.00 | 320 | 5'300 |
| Schwenker | LFE | 215.00 | 320 | 1'200 |
| Funke | LFE | 20.00 | 320 | 240 |
| Mammut | LFE | 4'000.00 | 315 | 39'000 |
| Vektor | LFE | 1'000.00 | 315 | 18'000 |
| Ameise | LFE | 2.00 | 315 | 110 |
| Hauptsegel | LFE | 1'500.00 | 310 | 13'000 |
| Rotluchs | LFE | 400.00 | 310 | 2'000 |
| Autark | LFE | 240.00 | 310 | 1'100 |
| Welpe | LFE | 32.00 | 310 | 800 |
| Mastodon | LFE | 1'350.00 | 305 | 8'000 |
| Bumms | LFE | 120.00 | 305 | 820 |
| Zwillingssau | LFE | 2'000.00 | 300 | 17'000 |
| Kodiak | LFE | 260.00 | 300 | 1'100 |
| Schraube | LFE | 16.00 | 290 | 230 |
| Spinne | LFE | 2.00 | 290 | 120 |
Flugzeug-Triebwerke
| Name | Typ | NN Schub | NN Isp | Vak. Schub | Vak. Isp | Kosten |
|---|---|---|---|---|---|---|
| Goliath | AFE | 360.00 | 12'600 | 2'600 | ||
| Huuuui | AFE | 120.00 | 10'500 | 1'400 | ||
| Panther | AFE | 85.00 | 9'000 | 130.00 | 4'000 | 2'000 |
| Juno | AFE | 20.00 | 6'400 | 450 | ||
| Peitsche | AFE | 130.00 | 4'000 | 2'250 | ||
| R.A.P.I.E.R. | AFE | 105.00 | 3'200 | 162.30 | 275 | 6'000 |
Kerbals
Erfahrungspunkte
Die Kerbals sammeln, je nach Spieleinstellung/-Modus, Erfahrungspunkte. Diese schalten Fähigkeiten frei die sehr nützlich sind. Folgender Flugplan stellt sicher, dass die Kerbals die maximale Stufe erreichen. Es sind alles Missionen, die mit LowTech im EarlyGame machbar sind.
| Missionsziel | Erfahrungspunkte | Erfahrungsstufe |
|---|---|---|
| Kerbin Orbit | 2.00 | 1 |
| Mun Flagge | 7.00 | 1 |
| Minmus Flagge | 13.25 | 2 |
| Eve Orbit, Gilly Flagge | 39.75 | 4 |
| Duna Flagge, Ike Flagge | 64.75 | 5 |
| Stufe | Pilot | Techniker | Wissenschaftler | |
|---|---|---|---|---|
| Navigation | Reparatur | Abbau | Forschung | |
| 1 | Vor-/Rückläufig | Fallschirme | 45% | 5x |
| 2 | Normal/Radial | Beine | 65% | 9x |
| 3 | Ziel/Manöver | Räder | 85% | 13x |
| 4 | - | - | 105% | 17x |
| 5 | - | - | 125% | 21x |
Forschung
Forschungsstation
Wo man eine Forschungsstation platziert hat durchaus einen Einfluss auf die Erzeugung der Wissenschaftspunkte. Wir erhalten einen Malus auf der Oberfläche von Kerbin von 90%. Also eine Forschungsstation auf Kerbin zu platzieren ist nicht wirklich sinnvoll. Vor allem, da wir bereits das Forschungszentrum haben. Es gibt einen Bonus von 25%, wenn wir die Daten in der Einflusssphäre des entsprechenden Objektes analysieren. Wenn man bei fehlenden Daten einfach nochmals aus dem Fenster schauen kann, hilft es extrem. Auf einer Oberfläche gibt es einen Bonus von 10%. Vermutlich wird den Kerbals weniger übel auf einem Planeten als wenn man irgendwo im All herumschwirrt. Und es erhöht die Motivation, wenn man kurz die Füsse vertreten kann. Beides kombiniert gibt den höchsten Bonus. Also sollte man immer dort, wo man die Daten her hat, diese auch analysieren. Da die 10% Bonus für die Landung nicht sehr viel sind, im Vergleich zum Mehraufwand, ist es am effizientesten, die Daten im Orbit zu analysieren.
Grenzen
Es gibt "unsichtbare" Grenzen in den Atmosphäre und der Einflusssphäre der Objekte, welche man separat erforschen kann. Die folgende Tabelle listet diese Grenzen auf, so dass man gezielter Missionen fliegen kann.
| Himmelskörper | Atmosphäre | Weltraum |
|---|---|---|
| Kerbol | 18'000m | 1'000'000'000m |
| Moho | - | 80'000m |
| Eve | 22'000m | 400'000m |
| Gilly | - | 6'000m |
| Kerbin | 18'000m | 250'000m |
| Mun | - | 60'000m |
| Minmus | - | 30'000m |
| Duna | 12'000m | 140'000m |
| Ike | - | 50'000m |
| Dres | - | 25'000m |
| Jool | 120'000m | 4'000'000m |
| Laythe | 10'000m | 200'000m |
| Vall | - | 90'000m |
| Tylo | - | 250'000m |
| Bop | - | 25'000m |
| Pol | - | 22'000m |
| Eeloo | - | 60'000m |